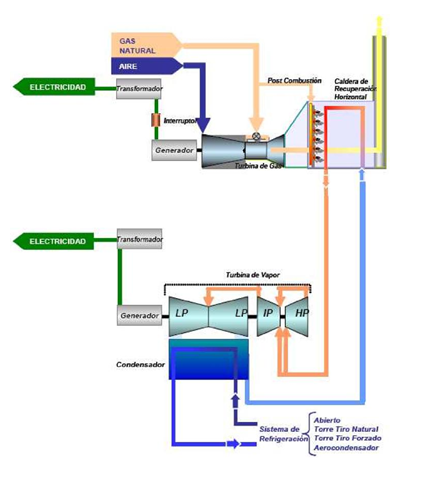
1. CICLO TERMODINÁMICO DE LAS TURBINAS DE GAS

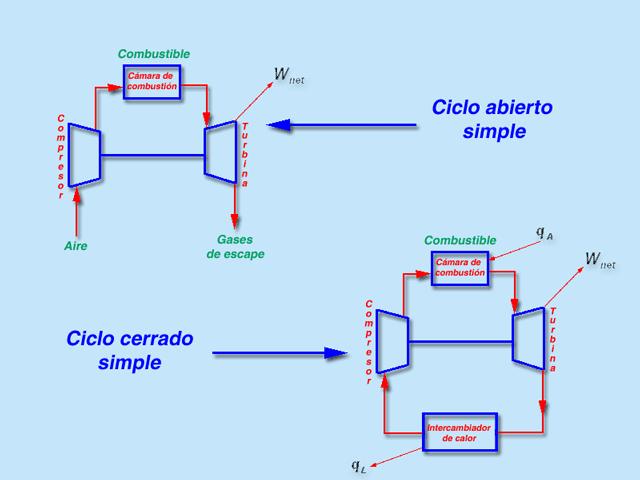
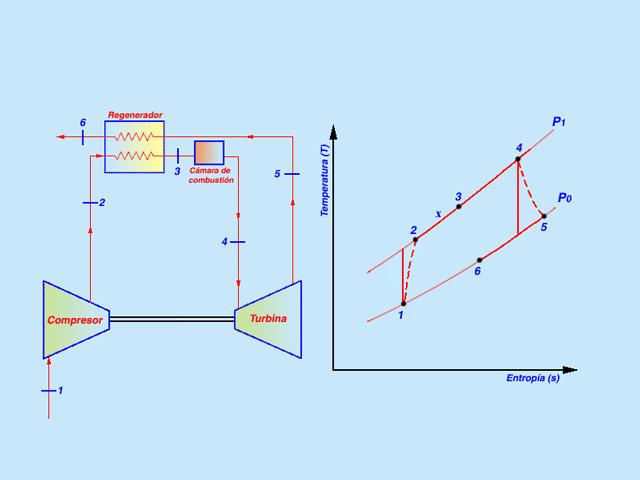
El modelo termodinámico de las turbinas de gas se fundamenta en el ciclo de Brayton, a pesar de que se generaliza como ciclo termodinámico, en realidad el fluido de trabajo no cumple un ciclo completo en las turbinas de gas ya que este finaliza en un estado diferente al que tenía cuando inició los procesos, se podría decir que es un ciclo abierto. Las turbinas de gas de ciclo abierto simple utilizan una cámara de combustión interna para suministrar calor al fluido de trabajo y las turbinas de gas de ciclo cerrado simple utilizan un proceso de transferencia para agregar o remover calor del fluido de trabajo.

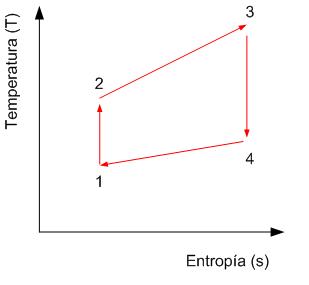
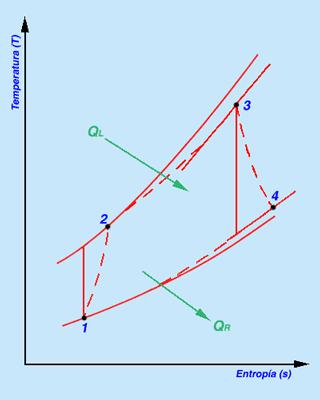
El ciclo básico de Brayton en condiciones ideales está compuesto por cuatro procesos:

• 1-2. Compresión isentrópica en un compresor.
• 2-3. Adición de calor al fluido de trabajo a presión constante en un intercambiador de calor o una cámara de combustión.
• 3-4. Expansión isentrópica en una turbina.
• 4-1. Remoción de calor del fluido de trabajo a presión constante en un intercambiador de calor o en la atmósfera.

En el ciclo Brayton, el trabajo neto realizado por unidad de masa es la diferencia entre el trabajo obtenido en la expansión y el trabajo invertido en la compresión, es decir:

 

Wnet = Wt - Wc

 

Para un gas ideal, el trabajo neto puede escribirse como:

 

Wnet = Wt - Wc

 

Y el calor de adición por unidad de masa será:

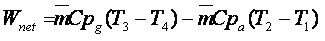
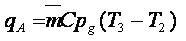
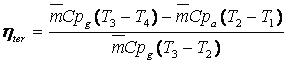
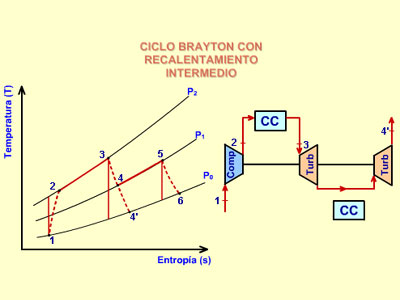
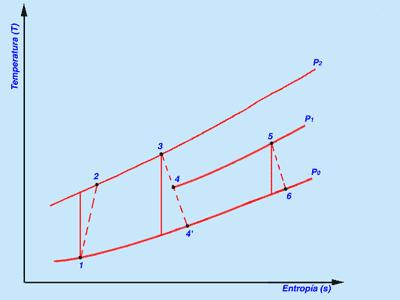
2. MODIFICACIONES CICLO BÁSICO EN LAS TURBINAS DE GAS

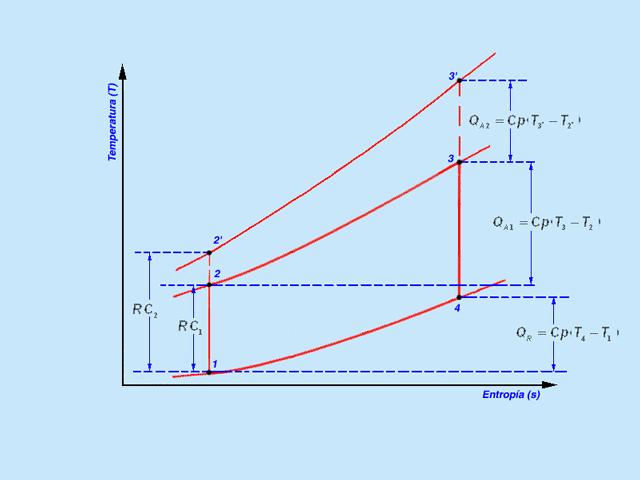
La eficiencia térmica del ciclo Brayton ideal depende de la compresión. Si se aumenta la relación de compresión en el ciclo será necesario suministrar más calor al sistema debido a que las líneas de presión constante divergen hacia arriba y hacia la derecha en el diagrama T-s y la temperatura máxima del ciclo será mayor. Como el calor suministrado es mayor, la eficiencia térmica aumentará con el ratio de compresión.

Sin embargo la temperatura máxima del ciclo está limitada por los materiales en los cuales están construidos los componentes y por lo tanto se requerirán sistemas de refrigeración más eficientes.

 

La eficiencia del ciclo también se ve afectada por las pérdidas en el compresor, en la turbina y en las caídas de presión en la cámara de combustión y otros pasajes. Podemos verlo en el diagrama que representa estas condiciones en el ciclo, disminuyendo en consecuencia la eficiencia del ciclo.

A diferencia del ciclo Ranking, el proceso de compresión para elevar la presión en el ciclo Brayton requiere un gran consumo de energía y gran parte del trabajo producido por la turbina es consumido por el compresor, en un porcentaje que puede estar entre 40% y 80%. Esta desventaja frente al ciclo Ranking hace necesario prestar una mayor atención en el diseño de turbinas de gas ya que cualquier pérdida de presión en la cámara de combustión y demás componentes entre el compresor y la turbina debe compensarse con mayor trabajo en el compresor. Adicionalmente, la eficiencia del compresor y la turbina juegan un papel muy importante, debido a que eficiencias cercanas al 60% en estos componentes ocasionarían que todo el trabajo producido por la turbina sea consumido por el compresor y por tanto la eficiencia global sería cero.

 

Es posible hacer algunas modificaciones al ciclo Brayton básico para obtener valores más favorables de eficiencia térmica y trabajo neto. Las modificaciones que podemos hacer son las siguientes:

 

2.1. CICLO CON ENFRIAMIENTO INTERMEDIO DEL AIRE

 

Con este método lo que hacemos comprimir los gases de admisión en dos etapas con una refrigeración intermedia, para sacar parte del calor que han adquirido en la primera etapa de compresión. La representación de estos procesos se muestra en la siguiente figura:

De la secuencia anterior, es claro que el trabajo que debe realizar el compresor para elevar la presión desde el estado 1 hasta el estado 2’ sin enfriador, es mayor que el trabajo que deben hacer los compresores con la misma eficiencia para elevar la presión del aire desde el estado 1 al 2 y del estado 3 al 4 con un enfriador de aire intermedio. Esta disminución en el trabajo total de compresión se debe a que las líneas de presión divergen hacia la derecha del gráfico T-s.

 

Se ha demostrado que el trabajo de compresión con enfriador es menor cuando la relación de presiones en las dos etapas es igual (P4/P3)= (P2/P1) y la temperatura de entrada a la segunda etapa de compresión (T3) es igual a la temperatura de entrada a la primera etapa de compresión (T1).

 

Al tener un menor trabajo de compresión, el trabajo neto del ciclo con enfriador será mayor que el trabajo neto del ciclo sin enfriador, siendo:

 

Wnet (sin enfriado) = Cpg (T5 – T6) – Cpa (T2’ – T1)

 

Wnet (con enfriado) = Cpg (T5 – T6) – Cpa ((T2 – T1) + (T4 – T3))

 

Como, 

Cpa ((T2 – T1) + (T4 –T2)) < Cpa (T2’ – T1)

 

Entonces,

 Wnet (sin enfriador) < Wnet (con enfriador)

 

Por otro lado, se requiere suministrar una mayor cantidad de calor al ciclo con enfriador para aumentar la temperatura desde (T4) hasta (TS) que en el ciclo sin enfriador, donde únicamente es necesario elevar la temperatura desde (T2’) hasta (TS).

En el diagrama T-s, puede apreciarse que la cantidad de calor adicional agregada al sistema, es mayor que la equivalente en calor del trabajo ahorrado por el compresor cuando trabaja con el enfriador de aire y por lo tanto la eficiencia térmica del ciclo con enfriador será menor que sin enfriador.

 

  ηter (sin enfriador) > η ter (con enfriador)

  

2.2. CICLO CON RECALENTAMIENTO INTERMEDIO

 

La expansión de los gases en el ciclo Brayton puede configurarse de tal forma que se realice en dos etapas. La primera expansión ocurre en lo que se conoce como turbina de alta presión (HP) o turbina del compresor (CT) acoplada al compresor mediante un eje. Todo el trabajo desarrollado por la turbina de alta presión es consumido por el compresor. La segunda expansión tiene lugar en la turbina de baja presión (LP) o turbina de potencia (PT) acoplada a un eje diferente al de la turbina del compresor y produce el trabajo neto aprovechado en varias aplicaciones, como para mover el generador.

En el ciclo con recalentamiento se instala una segunda cámara de combustión a la salida de la turbina de alta presión para elevar la temperatura de los gases que entran a la turbina de baja presión, y como  estos gases todavía son ricos en oxigeno no suele hacer falta un aporte extra de comburente.

 

La representación de estos procesos se muestra en la siguiente secuencia.

En la secuencia anterior, se puede observar que el trabajo de compresión es el mismo para el ciclo con recalentamiento que para el ciclo sin recalentamiento y en consecuencia el trabajo desarrollado por la turbina de alta presión será también igual para los dos ciclos. Sin embargo, el trabajo desarrollado por la turbina de baja presión es claramente mayor para el ciclo con recalentamiento que para el ciclo sin recalentamiento, debido a que las líneas de presión divergen hacia la derecha del diagrama T-s siendo mayor la diferencia entre las temperaturas (T5) y (T6) que entre las temperaturas (T4) y (T4’).

El trabajo neto desarrollado por cada unidad de masa de gas en el ciclo es el trabajo desarrollado por la turbina de baja presión e igual a:

 

Wnet (sin recalentamiento) = Cpg (T4- T4’)

 

Wnet (con recalentamiento) = Cpg (T5 – T6)

 

Debido a que T5 – T6 > T4 – T4’, entonces:

 

Wnet (sin recalentamiento) <Wnet (con recalentamiento)

 

A pesar de que hay un incremento en el trabajo neto desarrollado en el ciclo con recalentamiento por cada unidad de masa de gas, una cantidad de calor adicional debe suministrarse al sistema para elevar la temperatura de los gases que salen de la turbina de alta presión.

En el diagrama T-s, puede apreciarse que la cantidad adicional de calor Cp (TS -T4) suministrada al ciclo con recalentamiento es mayor que el aumento del trabajo neto desarrollado por la turbina y por lo tanto, la eficiencia térmica del ciclo con recalentamiento será menor que sin recalentamiento.

 

 ηter (con recalentamiento) > η ter (sin recalentamiento)

 

2.3. CICLO REGENERATIVO

 

En ocasiones se presenta que la temperatura de los gases a la salida de la turbina en el ciclo  Brayton es mayor que la temperatura del aire a la salida del compresor.

 

El ciclo regenerativo aprovecha esta diferencia de temperaturas para transferir a un regenerador o intercambiador de calor, energía térmica de los gases que salen de la turbina, al aire que sale del compresor.

En el caso representado en el diagrama T-s, la temperatura (Ts) de los gases que salen de la turbina en el estado 5 es mayor que la temperatura (T2) del aire que sale del compresor en el estado 2. En el regenerador, los gases ceden su calor al aire comprimido desde el estado 5 hasta el estado 6 cuando son evacuados a la atmósfera. En el caso ideal, el aire comprimido en el estado 2 tendrá la misma temperatura de los gases en el estado 6 y de igual manera la temperatura del aire en el estado 3 será la misma que la de los gases en el estado 5. En consecuencia, el calor suministrado en la cámara de combustión será únicamente el necesario para elevar la temperatura de (T3) a (T4) y no de (T2) a (T4).

 

El trabajo neto desarrollado en el ciclo regenerativo 1-2-3-4-5-6, es el mismo que en el ciclo Brayton simple 1-2-4-1 ya que le trabajo realizado por el compresor y el trabajo producido por la turbina no varía en los dos casos. Sin embargo, al requerirse un menor calor de adición para elevar la temperatura al valor máximo del ciclo (T4), se obtendrán eficiencias térmicas más favorables para el ciclo regenerativo.

 

Siendo:

η ter= Wnet / qA

 

Wnet (con regeneración) = Wnet (sin regeneración)

 

qA (con regeneración) < qA (sin regeneración)

 

Entonces:

 ηter (sin regeneración) > η ter (con regeneración)

 

En el caso ideal, se considera que una diferencial infinitesimal en la diferencia de temperatura es  suficiente para que el calor fluya en el regenerador de los gases que salen de la turbina al aire que sale del compresor. En el caso real, se requiere más que una diferencia infinitesimal y por lo tanto no se puede decir que (T3) es igual a (T5), ni que (T2) es igual a (T6). La diferencia de temperaturas (T3 – Tx) requerida por el regenerador para transferir energía térmica de un fluido al otro define su eficiencia:

 

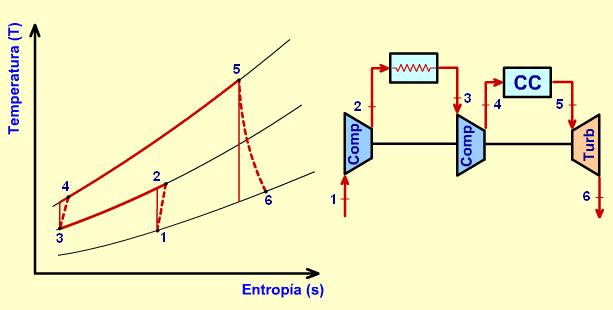
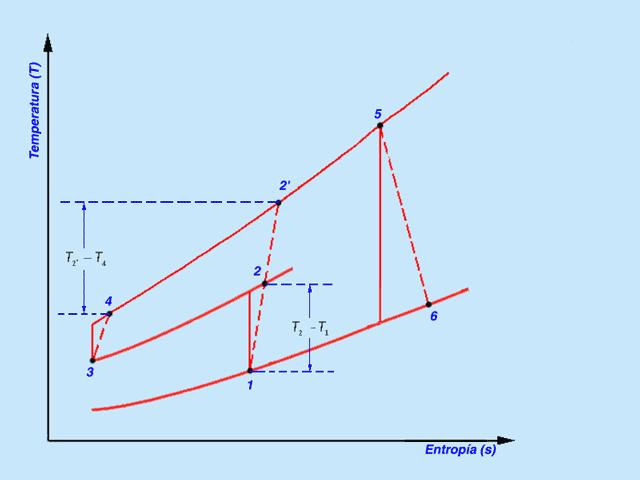
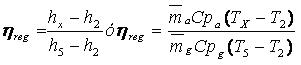
Si el flujo másico y los calores específicos del aire y el gas se suponen similares, es decir, ma ≈ mb  y  Cpa≈ Cpg, entonces:

 ηreg = (Tx – T2)/ (T5-T2)

Cuanto mayor sea la diferencia de temperaturas (T3 – Tx), menor será la diferencia (Tx – T2) y en consecuencia la eficiencia del regenerador será menor.

La selección del regenerador o intercambiador de calor debe ser un ejercicio cuidadoso ya que la eficiencia de éste puede mejorarse aumentando el área de transferencia y en consecuencia la caída de presión será mayor perjudicando la eficiencia térmica del ciclo.

Referencia: http://www.uamerica.edu.co/tutorial/4turgas.htm